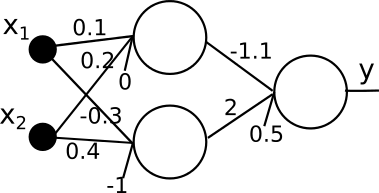
Neurális hálózat megvalósítása és tanítása
A feladat
1. Készítsen egy programot NNSolutionOne néven, mely egy adott architektúrájú neurális hálózat súlyait és bias értékeit inicializálja. A súlyok inicializálása történjen nulla várható értékű, 0.1 szórású normális eloszlásból sorsolt véletlen számokkal. A bias értékek 0-val legyenek inicializálva. (1 pont)
2. Készítsen egy programot NNSolutionTwo néven, amely a bemenetként kapott neurális hálózat (MLP) architektúra leírás, neurális hálózat súlyok és bemeneti értékek alapján kiszámolja a neurális hálózat kimenetét! (2 pont)
3. Valósítsa meg a hibavisszaterjesztés algoritmusát, és egészítse ki a programot NNSolutionThree néven úgy, hogy az a bemenetként kapott neurális hálózat architektúra leírás, neurális hálózat súlyok és bemeneti értékek alapján kiszámolja a neurális hálózat egyes súlyainak és biasainak hatását a kimenetre nézve (parciális deriváltak)! (2 pont)
4. Valósítsa meg a neurális hálózat tanítását. Egészítse a programot NNSolutionFour néven úgy, hogy az képes legyen a bemenetként kapott neurális hálózat architektúra leírás, tanítási paraméterek, neurális hálózat súlyok, valamint egy tanítóminta-készlet alapján a hálózat tanítására és validációjára! (2 pont)
5. A kiadott spam email osztályozási tanítóminta-készlet alapján és az 1. és 4. feladatrész felhasználásával hozzon létre és tanítson meg egy neurális hálózatot, ami minél kisebb hibával képes a tanítómintákhoz hasonló emailek osztályozására. A tanítási paramétereket valamint a neurális hálózat architektúráját és kezdeti súlyait szabadon megválaszthatja. Ezek megfelelő beállítása szükséges a feladat sikeres megoldásához (lásd: részletek). A feladat ellenőrzéséhez a megtanított neurális hálózatot nn_solution_five.txt néven kell beküldeni, mely a 2. részfeladat megoldásával lesz értékelve. (8 pont - ha az összes előző feladatrész is megoldásra került)
Segédlet a feladat megoldásához
Ajánlott a fenti segédlet átnézése, mivel a feladat megértését és megoldását nagymértékben megkönnyítheti.
Bemenet
A programok a standard inputról olvassák a bemenetüket. A feladatrészek szerint több különböző fajta bemenet lehetséges.
Architektúra
A neurális hálózat architektúráját írja le. A sorban egész számok szerepelnek (2-10 db) vesszővel elválasztva, melyek a neurális hálózat rétegeinek méreteit jelölik. Az első érték a bemeneti dimenziók száma N (1-100), utána jönnek a rejtett rétegek Li (1-100) neuronszámai, majd az utolsó érték a kimeneti dimenziók száma M (1-100).
Példa:
Neurális hálózat súlyok
A neurális hálózat súlyai a következő formában kerülnek átadásra. Minden sorban egy neuronhoz tartozó súlyok értékei szerepelnek, vesszővel elválasztva. Minden neuronhoz az előző réteg mérete + 1 súlyérték tartozik, ahol az i. érték az előző réteg i. neuronjának kimenetét súlyozza, az utolsó érték pedig a bias. A neuronok rétegek szerinti sorrend szerint következnek, a bemenettől a kimenet irányába, beleértve a kimeneti réteget is.
Példa:
Bemeneti értékek, kimeneti értékek, és tanítóminták
A neurális hálózat bemenete és tanítómintáinak leírása a következőképp néz ki. Az első sorban egy egész szám, S (1-10000) található, ami a bemeneti értékek vagy tanítóminták száma.
A következő S sor a bemeneti értékeket, vagy tanítómintákat tartalmazza, feladattól függően. Bemeneti értékek esetén (kívánt válasz nélkül) minden sor egy N elemű vektort tartalmaz (N jelentését lásd fent), azaz pontosan N valós számot, vesszővel elválasztva.
Tanítóminták esetén N+M valós számot tartalmaz minden sor. Ezek közül az első N érték a tanítóminta bemeneti részét, a fennmaradó M érték pedig a kívánt kimeneti részét jelentik.
Amennyiben a feladatrész a neurális hálózat kimenetét várja eredményül, a kimenetnek az S értéket követően a következő S sorban, a bemenetnek megfelelő sorrendben, a bemenetekre adott kimeneteket kell írni, melyek soronként pontosan egy M elemű vektort, azaz M valós értéket tartalmaznak, vesszővel elválasztva.
Tanítási paraméterek
A tanítási eljárás paramétereit egy sor írja le. Ebben a következő három érték szerepel vesszővel elválasztva: E a tanítási epochok száma (1-10000), mely azt jelenti, hogy a teljes tanítókészletet hányszor használjuk fel a tanítás során, a μ bátorsági faktor, mely a súlymódosítások mértékét jelenti, illetve R (0-1) valós szám, ami a tanítóminták aránya az összes mintára nézve. A fennmaradó minták validációs minták lesznek (lásd: 4. részfeladat).
Kimenet (standard output, stdout)
A programok a standard outputra írják a kimenetüket. A feladatrészek szerint több különböző fajta kimenet lehetséges. A kimeneti formátumok azonosak a bemeneti formátumokkal.
Átlagos négyzetes hibák
A tanítás során a validációs mintakészleten mérjük a hálózat általánosító-képességét. A tanítás pontosan E epochig tart. A validációs készlet átlagos négyzetes hibáját minden epoch végén kell kiszámítani, és kiírni egy új sorba. Azaz pontosan E sort kell kiírni, mindegyikbe pontosan 1 valós számot.
A feladatok részletei
NNSolutionOne
A program a következő sorrendben kapja a bemeneteket: architektúra
A programnak a következő sorrendben kell a kimenetre kiírni: architektúra, súlyok
A neurális hálózat súlyainak inicializálása egy nagyon fontos kérdés. Gondoljunk bele abba, mi történne, ha minden súly ugyanarra az értékre lenne inicializálva: nem lenne különbség az egyes neuronok között, hiszen minden neuron egyformán, az előző réteg összes kimenetéről ugyanazokkal az értékekkel súlyozva számolná ki a saját kimenetét, melyek között emiatt nem lenne különbség. A gradiens eljárás során pedig szintén nem tudnánk köztük különbséget tenni, ugyanazokat a súlymódosításokat hajtanánk rajtuk végre. Emiatt fontos, hogy minden neuron minden súlya különböző súlyértékekkel legyen inicializálva.
A súlyok kezdeti értékének nagysága erősen befolyásolja a tanítás konvergenciájának sebességét. Érdemes a súlyokat úgy inicializálni, hogy a súlyozott összegek az aktivációs függvény nemlineáris szakaszához közel essenek. Erre egy ökölszabály a 0 várható értékű, 0.1-es szórású normális eloszlásból vett véletlen számokkal történő inicializálás. Ez természetesen csak akkor megfelelő, ha a bemeneti mintavektorok elemeinek eloszlása szintén 0 várható értékű és egységnyi szórású. Ennek ellenőrzésétől, illetve a bemeneti minták normalizálásától jelen feladatban eltekintünk. Ennél a módszernél vannak kifinomultabb inicializálási eljárások is, melyek főleg sok rejtett réteget tartalmazó hálózatok esetén előnyösek (Xavier inicializálás), azonban ezekkel most nem foglalkozunk.
Példa bemenet és a hozzá tartozó kimenet:
2,3,1 |
2,3,1 0.07694805,-0.04505534,0.0 0.07036076,-0.008341249,0.0 -0.064064674,0.1687909,0.0 0.049475513,0.05999728,0.059059735,0.0 |
NNSolutionTwo
A program a következő sorrendben kapja a bemeneteket: architektúra, súlyok, bemenetek
A programnak a következő sorrendben kell a kimenetre kiírni: kimeneti értékek
A neurális hálózat kimenetének kiszámításakor, valamint a többi részfeladatban is a rejtett rétegbeli neuronok esetén ReLU ( f(x)=max(0,x) ) aktivációs függvényt alkalmazzon, a kimeneti rétegben pedig lineáris neuronokat használjon.
Példa bemenet és a hozzá tartozó kimenet:
2,3,1 1,0,-0.5 0,1,-0.5 1,1,-1 2,2,-2,0 4 0,0 0,1 1,0 1,1 |
4 0.0 1.0 1.0 0.0 |
NNSolutionThree
A program a következő sorrendben kapja a bemeneteket: architektúra (M=1), súlyok, bemenek (S=1)
A programnak a következő sorrendben kell a kimenetre kiírni: architektúra, súlyok és biasok helyén a parciális deriváltak
A feladat kiszámolni a neurális hálózat a megadott bemenetre adott kimenetének a súlyok és bias értékek szerinti parciális deriváltjait. A neurális hálózat kimenetének kiszámítását felfoghatjuk egy függvényként: y = MLP(x,w,b). Ennek a függvénynek a w és b (súlyok és biasok) szerinti parciális deriváltjainak az x helyen felvett értékét kell kiszámítani ebben a részfeladatban. Ezeket a parciális deriváltakat fogjuk felhasználni a következő részfeladatban a súlymódosításokhoz.
A parciális deriváltak kiszámítását mindenképpen analitikusan végezze. Használja ki a láncszabályt: a gyorsabb számítás érdekében a köztes számítási eredményeket tárolja el a backpropagation algoritmusnak megfelelően.
A véges differenciák módszerével ellenőrizheti, hogy az analitikus számítás megfelelő -e. Ez nem kötelező, de ajánlott. A ReLU deriváltja nem létezik az x=0 helyen. A gyakorlatban ez nem jelent gondot: az egyértelműség kedvéért legyen ReLU'(0)=0.
Példa bemenet és a hozzá tartozó kimenet:
|
2,3,1
1,0,-0.5
0,1,-0.5
1,1,-1
2,2,-2,0
1
0.75,0.75
|
2,3,1
1.5,1.5,2.0
1.5,1.5,2.0
-1.5,-1.5,-2.0
0.25,0.25,0.5,1.0
|
NNSolutionFour
A program a következő sorrendben kapja a bemeneteket: tanítási paraméterek, architektúra, súlyok, bemeneti minták
A programnak a következő sorrendben kell a kimenetre kiírni: átlagos négyzetes hibák, architektúra, súlyok
A tanítás során a bemeneti minták csak egy részét használja tanításra. Ez a rész a minták száma (S) és a tanítómintaarány (R) szorzatának alsó egészrésze, St=floor(S*R). Tanítómintának válassza a bemeneti minták közül az első St darabot. A fennmaradó minták ún. validációs minták lesznek Sv=S-St.
A tanítómintákat sorban egymás után vegye, epochonként pontosan egyszer. A súlymódosítást a delta szabállyal végezze minden tanítómintára egyenként, vagyis a súlyokat a hiba súlyok szerinti parciális deriváltjának bátorságifaktor-szorosával módosítsa. Ez a legegyszerűbb, ún. sztochasztikus gradiens algoritmus, melynek vannak bizonyos hátrányai, azonban ennél kifinomultabb eljárások elsajátítására (pl. minibatch) a tárgy korlátos ideje miatt nincs lehetőség.
Az epoch végén, tehát mikor az St tanítóminta mindegyikével elvégzett egy tanítási lépést, értékelje ki a neurális hálózatot a validációs mintákkal: számítsa ki a hálózat kimenetét mindegyik validációs mintára, majd a validációs minták kívánt válaszai alapján számítsa ki az átlagos négyzetes hibát, a validációs minták (Sv) és a kimenetek (M) szerint átlagolva.
Példa bemenet és a hozzá tartozó kimenet:
1,0.1,0.5 2,3,1 1,0,-0.4 0,1,-0.5 0.9,1,-1 2,1.9,-2,0 8 0,0,0 0,1,1 1,0,1 1,1,0 0.2,0.2,0 0.2,0.8,1 0.8,0.2,1 0.8,0.8,0 |
0.17536075
2,3,1
0.8978304,-0.018169597,-0.5021696
-0.017527387,1.0014727,-0.4985274
0.9184014,1.0184015,-0.98159856
1.9708253,1.9000499,-2.0082808,-0.041200735
|
nn_solution_five.txt
A fájlnak a következő sorrendben kell tartalmaznia a megtanított neurális hálózat paramétereit: architektúra, súlyok
(gyakorlatilag a 4. részfeladat kimenetének vége)
A kiadott adatkészlet (tanítókészlet) a klasszikus spambase adatkészletből származik, mely egy spam email osztályozási probléma. A feladat az, hogy az emailek bizonyos tulajdonságai alapján megállapítsuk, hogy az adott email spam -e vagy sem. A tulajdonságok, melyek alapján az osztályozást végezzük, számunkra nem fontosak, de akit érdekel, hogy mik ezek a tulajdonságok, az itt elolvashatja. A spambase adatkészlet weboldalda itt található.
Az adatkészleteket tartalmazó fájl mind a 4500 sora egy-egy email 57 tulajdonságát tartalmazza, vesszőkkel elválasztva (első 57 oszlop). Az utolsó , 58. oszlopban az adott email osztálya szerepel, ami azt mondja meg, hogy az adott email spam email -e, vagy sem. A feladat egy olyan neurális hálózat tanítása, amely minél jobb eredménnyel képes osztályozni ezen tulajdonságok alapján olyan emaileket is, melyek nem szerepelnek a tanítókészletben.
A megoldás ellenőrzéséhez néhány, a tanítókészletben nem szereplő tesztminta felhasználásával teszteljük a beadott neurális hálózatot. A feladatrészre összesen maximum 8 pont kapható. A kapott pontszám a neurális hálózat teljesítményétől függ. 22% hibás osztályozási arányra 1 pont jár, minden további 2% javulás +1 pontot ér. 8% vagy az alatti hibaarány esetén a maximális 8 pont kapható.
Tippek a megoldáshoz
A feladat nem számít nehéznek, a megoldásához, a hálózat méretének és tanítási paramétereinek megválasztásához azonban többszöri próbálkozásra is szükség lehet. Vizsgáljon meg különböző méretű neurális hálózatokat (súlyok száma: 10-10000 között, 1-3 rejtett rétegbe elosztva), és ezeket tanítsa a tanítómintákkal.
A tanításnál ügyeljen a túltanulás/túlilleszkedés jelenségére. Ehhez ossza fel tanító és validációs mintákra a kiadott mintákat, például 80%-20% arányban. Az így kialakított tanítómintákkal tanítson, a validációs mintákat pedig a tanítás során a hálózat teljesítményének ellenőrzésére használa, de ne használja fel azokat tanításra. Amennyiben azt tapasztalja, hogy a validációs mintákon már nem csökken a hibaarány, a hálózat valószínűleg a túltanulás fázisában van, ilyenkor érdemes leállítani a tanítást, hiszen a hálózat általánosítóképessége nem lesz jobb, és szerencsétlen esetben akár romolhat is.
Tipikusan 250-5000 epoch lehet szükséges a tanításhoz. Ez az érték a bátorsági faktortól is függ. Egy ilyen hosszú tanítás a számítógép sebességétől és az implementáció hatékonyságától függően néhány perc - negyed óra időt is igénybe vehet.
A bátorsági faktor értékének megválasztásakor két dolgot tartson szem előtt: túl kicsi bátorsági faktorral indokolatlanul lassú lesz a tanítás. Túl nagy bátorsági faktorral pedig a tanítás akár divergálhat is (egyre nagyobb hibaértékek, végül NaN). Tipikus bátorsági faktor például: 0.01.
Példa a beküldendő fájlra:
|
57,2,1 |
Értékelés
A beadott megoldásokat automatikusan ellenőrizzük, és rövid időn belül visszajelzést adunk a helyességükről vagy hibákról. Ezután lehetőség van javításra és új program beküldésére. A tökéletes megoldások 15 pontot érnek. Tetszőleges számú megoldás beküldhető a feladat határidejének lejártáig. Az utoljára beküldött megoldásra kapott pontszám lesz az a végleges pontszám, amely a félév végi jegybe számít.
Technikai információk
A programot Java nyelven kell elkészíteni, és a HF portálon kell leadni a megadott határidőig.
A beküldött Java forráskódnak tartalmaznia kell a programnevekkel megegyező nevű osztályokat (tehát pl: NNSolutionOne, stb...), melyben megtalálható az adott részfeladatot megoldó main függvény. A program tetszőleges számú forrásfájlból állhat. A program nem használhat a standard inputon és outputon kívül semmilyen más erőforrást, így nem végezhet fájlműveleteket és nem nyithat hálózati kapcsolatokat.
Beadandó a programok forráskódja, valamit az 5. részfeladat neurális hálózatát leíró nn_solution_five.txt egy .zip fájlba tömörítve. A programokat automatikusan teszteljük, több különböző bemenettel, vagyis több különböző neurális hálózat architektúrával és tanítókészlettel. A kimeneten közölt neurális hálózat súlyértékeinek hibahatáron belül meg kell egyezniük a referencia implementáció értékeivel.
A beküldött forráskódoknak mind saját készítésűnek kell lennie, nem szabad felhasználni semmilyen külső forrást (beleértve más hallgató munkáját, interneten található osztálykönyvtárakat). Ez alól kivétel az Apache Math Commons könyvtár, mely lineáris algebra műveletekre felhasználható. A könyvtár használatához a szükséges osztályok forráskódjait kell beküldeni, nem pedig a .jar fájlt.
Figyelem! A beküldött megoldásokat a félév végén plágiumkeresésnek fogjuk alávetni. Minden, kétséget kizáróan azonos vagy részben azonos megoldás szerzőjétől megtagadásra kerül a tárgyból az aláírás.