Digitális eszközökkel történő minőségjavítás
A digitális eszközökkel történő feljavítás néhány tekintetben különbözik az előbb leírt módszerektől. A fizikai és analóg módszerekkel az eredeti lemezt, illetve az eredeti lemezről közvetlenül lejátszott hangot próbáljuk meg feljavítani. A digitális módszerek elszakadnak az eredeti hanghordozótól, ezáltal jóval több lehetőséget tudnak nyújtani.
Már a hetvenes években is próbáltak digitális eszközöket alkalmazni hangfelvételek minőségjavítására, amikor régi Caruso felvételek hangját próbálták csatornakiegyenlítéssel feljavítani [12]. A téma a Compact Disc megjelenésével került ismét előtérbe, amikor is a digitális technikával lehetővé vált a régi hangfelvételek időtálló archiválása. Azonban a sercegő, sistergő felvételek közvetlen átmásolása nem lett volna túl szerencsés, amikor a CD egyik legnagyobb előnye a szinte teljes csendből kiemelkedő hang. Ezért merült fel a régi hangfelvételek digitális módon történő minőségjavításának igénye. Ehhez először a hangfelvételt fizikai módszerekkel feljavítják annyira, amennyire csak lehet, majd a hanglemezt egy jó minőségű lemezjátszóval lejátszva a hangot digitalizálják. A digitálisan rögzített hangmintákon már különféle eljárások hajthatók végre. Végül a feljavított hangot CD-n rögzítik.
Egyetlen algoritmus nem lehet alkalmas minden zavar elnyomására, mert a hanglemezen fellépő zavaroknak nagyon eltérő a tulajdonságuk. A kattogás és sercegés típusú zavarok időben kis kiterjedésűek, ezért érdemes az egyes sercenéseket, kattanásokat megkeresni és csak azokat a mintákat módosítani, amelyek hibásak. Mivel egyik algoritmus sem képes arra, hogy egy általános hangjelet minden körülmények között képes legyen egy-az-egyben visszaállítani, így el lehet kerülni a hibát nem tartalmazó minták módosítását és ezáltal a zavart nem tartalmazó jelrészletek minőségének romlását. Az alapzaj és a zúgás ezzel szemben minden hangmintát módosít, ezért ezeknél másfajta algoritmusokra van szükség a zavar csillapításához. Ugyancsak eltérő algoritmust igényel a hangmagasság-ingadozás okozta zavar.
Rengeteg algoritmus született a zenei anyagok minőségének feljavításához. Az összes algoritmus áttekintése sajnos nem áll módunkban, az algoritmusok nagy száma miatt. Az algoritmusok nagy része ezenkívül nem is publikus. A következőkben csupán az általam készített zajcsökkentő programban alkalmazott sercegést csökkentő algoritmus alapjait fogom bemutatni. Azért esett erre a torzulásra a választásom, mert ezek a zaj minden feljavítást igénylő hanglemez-felvételen előfordul, továbbá erősen zavarja a műélvezetet, tehát fokozottan érdemes az eltávolításával foglalkozni.
A sercegések és kattanások eltávolításához először detektálni kell a sercenéseket és kattanásokat a hangfelvételben, meg kell határozni azok pontos kezdetét és végét, majd egy algoritmus segítségével elő kell állítani a zavar helyén az eredeti minta becslőjét [8], [13]. Először tehát megvizsgáljuk a detektálást és a helymeghatározást, majd a jelbecslő algoritmusokat.
Az alapzaj eltávolítását a frekvenciatartományban érdemes végezni. Ehhez előbb elő kell állítani egy zajbecslőt, majd a becslő segítségével a jel spektrumát módosítjuk [8]. Ehhez meg kell majd vizsgálni a zajbecslő előállítását és a zajszűrés módjait.
Időtartományban, felüláteresztő szűrés segítségével történő detektálás
A sercegés és kattanás típusú jelek detektálásához alkalmas paraméter az ilyen típusú jelekre jellemző nagyfrekvenciás oszcilláció. Ezt a paramétert felüláteresztő szűrőkkel érdemes kiemelni.
Az oszcilláció kiemeléséhez különféle elemszámú és paraméterű felüláteresztő lineáris fázisú FIR szűrőket próbáltam ki. Azért dolgoztam lineáris fázisú FIR szűrőkkel, mert IIR szűrők esetén a fellépő változó fáziseltolások és késleltetések megnehezítették volna a sercenések és kattogások határának detektálását.
Minél nagyobb elemszámú szűrőt próbáltam ki, annál nehezebbé vált a detektálás a szűrők tranziensei miatt. Ezek hozzáadódva a lemezhiba által okozott tranziensekhez, azokat jóval hosszabbnak mutatták. Ha az így meghatározott kattanás határok alapján dolgoznánk, rengeteg hasznos jelet is feleslegesen szűrnénk.
A legjobb eredményt a hátralépő differencia művelet szolgáltatta, amely a következő képlettel írható fel:
ahol 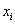 a jel i-edik mintája,
a jel i-edik mintája, 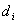 az i-edik differencia érték. A jelsorozat első eleméhez nem lehet differencia értéket előállítani, ezt egyszerűen 0-nak veszem.
az i-edik differencia érték. A jelsorozat első eleméhez nem lehet differencia értéket előállítani, ezt egyszerűen 0-nak veszem.
Az ilyen módon előállított jelsorozatot vizsgálva, a jelsorozatot a frekvenciaspektrum alapján történő detektáláshoz hasonlóan kisebb (kb. 1024 minta hosszúságú) szakaszokra bontva, a szakaszok abszolút értékét képezve (ez az energiafüggvény előállítását célozza) az egyes szakaszokba már be lehet húzni egy komparálási szintet, ami alapján megkülönböztethetők a tranziensekre jellemző értékek a többitől. A hátralépő differencia gyakorlatilag nem ad hozzá tranzienst a lemezhibák által okozott jelalakokhoz, így a hibák határai nagy pontossággal meghatározhatók. Az algoritmus további előnye a rendkívüli egyszerűsége és ezáltal a vele készíthető algoritmus nagy sebessége.
Jelminták becslése medián-szűréssel és a magas hangok becslésével
Egy általam kigondolt robosztus algoritmus a medián-szűréssel megvalósított jelminta becslés. A medián-szűrő a rendezett statisztikus szűrők egyik fajtája. Ezek a szűrők a szűrőablakban található mintákat érték szerint sorrendbe rakják, majd a rendezett elemek alapján visszaadnak valamilyen értéket. A medián-szűrő a rendezett elemek közül a középső elemet, azaz a mediánértéket adja vissza. Ezzel a szűrővel hatásosan csillapíthatók a környezetükből kiugró impulzus jellegű zavarok.
A sercegés impulzusai hatásosan csillapíthatók egy megfelelő méretű medián-szűrővel. Kis ablakkal rendelkező szűrő esetén a szűrés még nem elég hatásos, túl nagy méretű szűrőt használva viszont nem csak a sercenés impulzusokat szűrjük ki, hanem hasznos információt is. A sercenések átlagos hossza kb. 20-25 minta ha a zenei anyagokat 44.1 kHz mintavételi frekvenciával digitalizáljuk (ez egy elterjedt érték a gyakorlatban). A medián-szűrőnek is körülbelül ilyen hosszúnak kell lennie. Kísérleteket végezve a 21 elemű (0.476 ms ablak szélességű) medián-szűrővel végzett szűrés bizonyult optimálisnak.
A medián-szűrés segítségével így eltávolíthatók a sercenések impulzusai, azonban a sercenés helyén medián-szűréssel csupán a jel alapvonalát tudjuk helyreállítani, a sercenés helyén levő nagyfrekvenciás komponenseket nem. Az így helyreállított felvételben észlelhető, hogy a szűrés helyén a magas hangok rövid időre kiesnek. A sercegő hangzás ugyan megszűnik, de a magas hangok kiesése halk, papírzörgés-szerű hangként hallható. A magas hangokat is érdemes ezért ezeken a területeken becsülni.
A magas hangok becsléséhez állítsuk elő a hibás jelrészlet előtti, ép jelszakasznak is medián-szűréssel az alapvonalát, majd a kapott alapvonalat vonjuk ki az ép jelből. Az így kapott jelet illesszük rá a hibás jelszakaszon előállított alapvonalra. A határokon fellépő illesztetlenség elkerüléséhez állítsunk elő a hibás szakasz hosszánál kicsit hosszabb nagyfrekvenciás jelbecslőt, majd a sercenés határain túl az ép jelrészlettel átlapolódó szakaszokon végzett lineárisan vagy nemlineárisan súlyozott átlagolással az illesztetlenség megszüntethető (11. ábra).
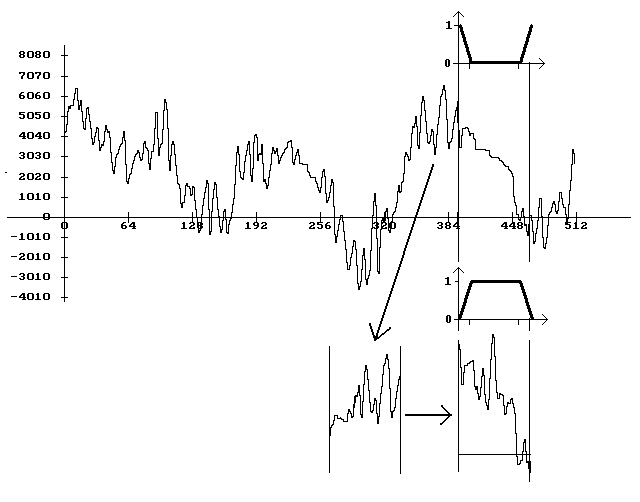
11. ábra A magas hang becslésének folyamata a medián-szűrt szakasznál
Az alapzaj szűrése digitális módszerekkel
Az alapzaj becslőjének előállítása
Az alapzaj, additív zaj. Mivel a zaj sztochasztikus jellegű, egymástól gyakorlatilag független mintákból áll, ezért az időtartományban nem sokat tudunk tenni, annál inkább viszont a frekvenciatartományban. Ha elő tudunk állítani egy becslőt a zaj teljesítménysűrűség-spektrumára és ezt �kivonjuk� a zajos jel teljesítménysűrűség-spektrumából, ilyen módon vissza tudunk állítani egy zajmentesített jelet. A becslő előállítása a zajos jel egy olyan részletéből történhet, amelyik csak zajt tartalmaz, hasznos jelet nem.
Az alapzaj sztochasztikus jel. A becslő, amit elő tudunk állítani, a teljesítménysűrűség-spektrum becslője, a periodogram. Azonban a sztochasztikus jelek teljesítménysűrűség-spektrumának becslője 100%-os relatív varianciájú, így közvetlenül nem alkalmazható[14]. A variancia csökkentése Welch-módszerrel történhet, azaz 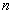 darab
darab 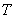 hosszúságú független mintaregisztrátumból meghatározunk M darab teljesítménysűrűség-függvény becslőt és az M becslő átlagát képezzük:
hosszúságú független mintaregisztrátumból meghatározunk M darab teljesítménysűrűség-függvény becslőt és az M becslő átlagát képezzük:
A becslés varianciája ekkor - független mintaregisztrátumokat feltételezve - az M-ed részére fog csökkenni
A Welch-módszer az ablakfüggvény alakját változatlanul hagyja. Hatékonysága tovább javítható, ha átlapolt regisztrátumokból származtatjuk a becslőket (módosított Welch-módszer).
Az alapzaj szűrése
A zajjal fedett jelek optimális helyreállítását, ha rendelkezésünkre áll a zaj és a hasznos jel teljesítményspektruma, Wiener-szűréssel tehetjük meg [8][14]. Hangfelvételek esetén sajnos nem áll módunkban meghatározni a hasznos jel teljesítményspektrumát, ezt legfeljebb csak becsülni tudjuk, ezt a becslőt azután ki kell vonnunk az eredeti jel periodogramjából:
ahol 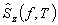 az általunk meghatározott alapzaj teljesítménysűrűség spektrumbecslő,
az általunk meghatározott alapzaj teljesítménysűrűség spektrumbecslő, 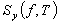 az eredeti zajos jel
az eredeti zajos jel
periodogramja, 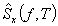 pedig az előállított zajszűrt periodogram.
pedig az előállított zajszűrt periodogram.
A módszer problémája, hogy 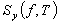 nagy varianciája miatt az
nagy varianciája miatt az 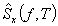 becslő nem pontos. Gyakran a becslő spektrumvonalai negatív értékűek. Ezt a problémát úgy szokás feloldani, hogy a kapott negatív értékeket nullával helyettesítjük [8]. Ezt a módszert hívják soft elbow algoritmusnak. A másik probléma, amikor a zajos jelben a zaj által keltett frekvenciakomponens nagyobb mint az alapzaj spektrumbecslő és így a eredmény spektrumban visszamarad a zajkomponens egy része (szintén a variancia miatt). A megszűrt hanganyagban ez a visszamaradt zajkomponens ugyan jóval kisebb, mint az alapzaj volt, viszont a kapott maradvány zajnak megváltozik a hangszíne: az egyenletes sziszegés helyett egy furcsa bugyborékoló, �kuruttyoló" hang jelenik meg, ami ugyan halkabb mint az alapzaj, azonban a hallgató számára zavaróbb lehet, mint az eredeti állandó jellegű sziszegés. Egy módosított algoritmus ezen úgy próbál segíteni, hogy nem változtatja meg azokat a spektrumvonalait az eredményspektrumnak, amelyek az eredeti zajos spektrumban nagyobbak mint az alapzaj spektrumbecslője, csak azokat az értékeket teszi nullává, amelyek kisebbek annál. Ekkor a zaj csökkenése ugyan kisebb, de a maradvány zaj nem tűnik fel annyira a megszűrt hangban. Ezt a módszert hard elbow algoritmusnak hívják.
becslő nem pontos. Gyakran a becslő spektrumvonalai negatív értékűek. Ezt a problémát úgy szokás feloldani, hogy a kapott negatív értékeket nullával helyettesítjük [8]. Ezt a módszert hívják soft elbow algoritmusnak. A másik probléma, amikor a zajos jelben a zaj által keltett frekvenciakomponens nagyobb mint az alapzaj spektrumbecslő és így a eredmény spektrumban visszamarad a zajkomponens egy része (szintén a variancia miatt). A megszűrt hanganyagban ez a visszamaradt zajkomponens ugyan jóval kisebb, mint az alapzaj volt, viszont a kapott maradvány zajnak megváltozik a hangszíne: az egyenletes sziszegés helyett egy furcsa bugyborékoló, �kuruttyoló" hang jelenik meg, ami ugyan halkabb mint az alapzaj, azonban a hallgató számára zavaróbb lehet, mint az eredeti állandó jellegű sziszegés. Egy módosított algoritmus ezen úgy próbál segíteni, hogy nem változtatja meg azokat a spektrumvonalait az eredményspektrumnak, amelyek az eredeti zajos spektrumban nagyobbak mint az alapzaj spektrumbecslője, csak azokat az értékeket teszi nullává, amelyek kisebbek annál. Ekkor a zaj csökkenése ugyan kisebb, de a maradvány zaj nem tűnik fel annyira a megszűrt hangban. Ezt a módszert hard elbow algoritmusnak hívják.
A szűrt felvételben visszamaradó alapzaj mennyiségét azzal is lehet csökkenteni, ha a zajszűréshez nem az eredeti zajbecslőt használjuk, hanem előbb annak minden spektrumvonalát megszorozzuk egy 1-nél nagyobb konstanssal. Ekkor jóval kisebb lesz a szűrt anyagban visszamaradó alapzaj értéke. További javulást érhetünk el, ha valahogyan figyelembe tudjuk venni az egyes zaj spektrumvonalak szórását és ennek megfelelően módosítjuk azokat a szűrendő felvételben.
A zajszűrés a következőképpen néz ki egy folyamatábrán:
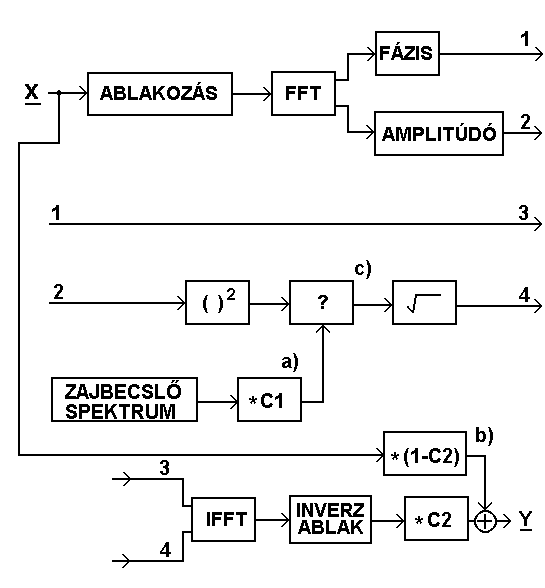
12. ábra Zajszűrés folyamatábrája
Az ábrán az a) pontnál látható a zajbecslő 1-nél nagyobb számmal történő szorzása, a b) pontnál pedig a zajszűrés hatásfoka állítható be. Ez azért hasznos, mert kisebb hatásfok esetén a zajszűrés során fellépő torzulások is kisebbek lesznek (bár most több zaj marad vissza a felvételben). Így a hatásfok segítségével beállítható egy olyan zaj/torzulás arány, amely sokkal kellemesebb hangélményt nyújt, mint az eredeti zajos hang, illetve a teljesen megszűrt hang. A c) pontnál, a �?�-lel jelzett dobozban az előbb elmondott hard elbow, vagy soft elbow algoritmus megvalósítása van.

