Student projects at the Department
Signal Model Based Synthesis of the Sound of Organ Pipes
Report based on results achieved during
Project laboratory,
Scientific Conference of Students (1st price (Faculty competition), 3rd price (National competition))
Master Thesis (Qualification: excellent, 1st prize of the Master Theses' competition arranged by the AES Hungarian Section and the OPAKFI Societies)
Project laboratory,
Scientific Conference of Students (1st price (Faculty competition), 3rd price (National competition))
Master Thesis (Qualification: excellent, 1st prize of the Master Theses' competition arranged by the AES Hungarian Section and the OPAKFI Societies)
1998-1999
Author: János Márkus, Advisor: László Sujbert, Ph.D.
| Introduction Prior Art The Signal Model Analysis Synthesis Results Demo Recordings Links |
 |
In the recent years digital sound synthesis and modeling become one of the most interesting research topic in the Digital Signal Processing laboratory at the Department of Measurement and Information Systems. In the laboratory, besides the basic instruments (PCs, signal generators, oscilloscopes, spectral analyzer, etc.) one can find development tools dedicated for digital signal processing. Such tools are the ADSP2181 fixed-point signal processing card from Analog Devices , the 56000 DSP-family from Motorola and some kits from Texas Instruments.
For off-line research and algorithm development, the MatLab environment is used.
This environment was the home of the organ sound synthesis project, which started during project laboratory and was partly finished in my Master Thesis.
The high-fidelity synthesis of the sound of the musical instruments is a long-standing problem for both the musicians and the acoustical engineers. The pipe-organ - with its building and maintenance costs - exceeds from the musical instruments. Thus, the organ is also in the centre of the synthesis research for a long while.
Laurens Hammond has developed the first organ-model in the begin of the thirties. The model - the legendary Hammond organ - uses several electro-mechanical sine wave generators to produce organ-like sound. As the technology has changed, the analog models become smaller and more economical, using first module circuits and later analog IC-s.
Since the late 70's, the digital synthesis techniques has been overshadowed gradually the analogue ones. Today's most prevalent method - called sampling or PCM - is the method used exclusively in the digital organs available on the market. The basis of the method is that the sound of the instrument is recorded, the record is compressed ("looped", taking into consideration the periodicity of the signal's stationary part) and stored. The method is more efficient if it also takes into account that the neighboring pitches of the instrument are nearly the same, so using resampling techniques, even more memory space could be saved. The greatest disadvantage of this method is that it cannot reproduce the stochastical behaviour of the instrument.
To eliminate the problems of the sampling synthesis a new synthesis method has been introduced in the 90's. The Physical Modeling (PM) tries to model not the sound, but the instrument itself. Using the instrument's parameters and its mathematical-physical relationships (based on the differential equations of the musical instrument), the sound of the instrument is calculable. The problem of this model is that a lot of redundant parameters has to be calculated, and it needs fast hardwares for real-time synthesis. In the case of using so-called semi-physical models, sometimes it is hard to find the transformation between the sound- and the model parameters.
There are also several other synthesis methods, but all of them are in an experimental state.
Signal model based synthesis could be a well-balanced compromise between the computation efficiency and the sound quality. In this case first both the deterministic and stochastic properties of the sound of an instrument are analyzed. Later, using the parameters come from the analysis, the reproduced sound become "high fidelity" if the model is accurate enough.
As most of the musical instruments generate nearly periodic sound, the signal model is based on the discrete-time model of the periodic signals.
From another point of view we have searched the answer to the following question: Is it possible to generate good-quality model using the classical, Fourier-expansion based (so-called additive) synthesis method, completed with some auxiliary part (such as modulators, noise-generators, filters, etc)?
The final organ-model has been set during the experiments (see also the next chapter). The model has three part with three different function (see Figure 1):
- "generator" part (the periodic model and a noise generator)
- "transient part" (responsible for the attack and decay transient behaviour of the sound, using independent IIR filters, as envelope-generators)
- "other effects" part (includes the effect of the different position of the sound, the effect of the hall (reverberation), etc.)
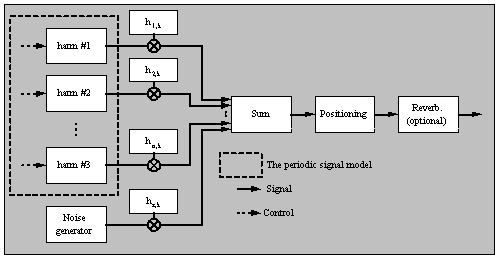 |
The parameters of the organpipe-models were derived off-line from original pipe-records. We have measured a lot of pipes from three different organs in order to get the quantitative characteristics of each register (series of pipes), and to set the significance of each parameter (e.g. the precision of modeling the transients).
 |
 |
 |
| Császár | Naszály | Tata |
Using a fully automatic analysis process, we could find both the determinisctic and stochastic numerical parameters. The whole process can be seen in Figure 3.
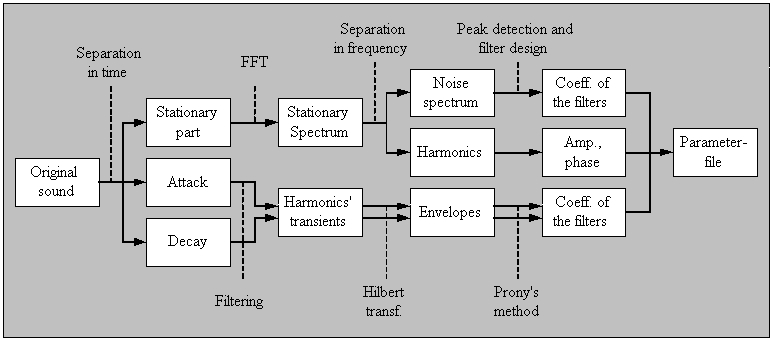 |
The synthesis - based on the measured parameters - has been implemented real-time and also off-line. First (during the project laboratory) we have used a Motorola 56001 Digital Signal Processor (DSP), later - to implement more feature - we have changed to an Analog Devices DSP. To make greater models, an off-line synthesis program under MATLAB has also been developed.
The block-diagram of the synthesis can be seen on Figure 4.
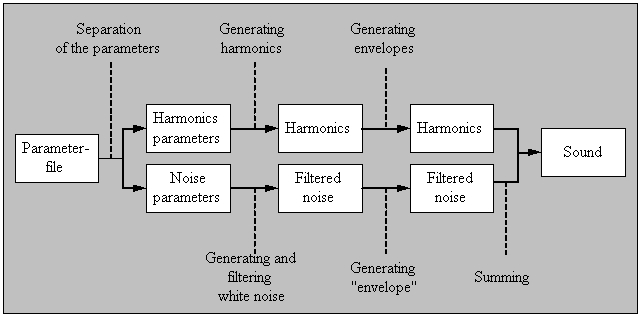 |
The efficiency of the proposed model can be introduced with demo recordings (see in the next chapter), as well as with some figures.
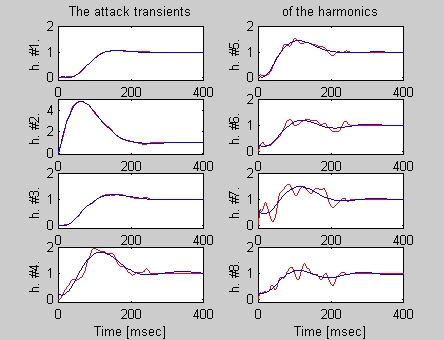
The following two pictures has been made using MATLAB. Figure 5. shows an original and model spectrum, while in Figure 6. the attack transients of an original and model pipe can be seen.
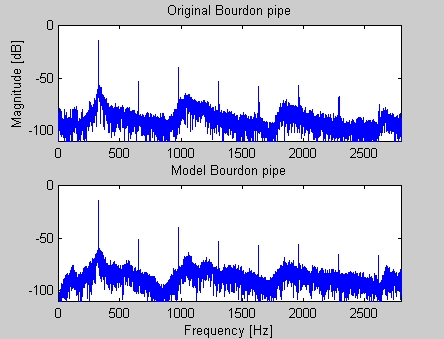 |
 |
The following links contain some demonstration records. One can compare original organ sound with its model, off-line simulation results of a bigger organ and real-time implementation of one Bourdon register.
The files are stored in mp3 format.
- J. S. Bach: Ich ruf zu Dir choral (part)
Matlab simulation, Stops: Diapason 8', Diapason 4', Bourdon 8', Octavbass 8', Subbass 16'. (Size: 495 kb, length: 30 sec) - J. S. Bach: Ach, was soll ich, Sünder, machen choral (part)
Original recordings in the Reformed church of Naszály, 1 Bourdon 8' stop. (Size: 513 kb, length: 32 sec) - J. S. Bach: Ach, was soll ich, Sünder, machen choral (part)
Matlab simulation, 1 Bourdon 8' stop. (Size: 512 kb, length: 32 sec) - J. S. Bach: F-major invention (part)
ADSP2181 DSP, real-time, 1 Bourdon 8' stop, 3 part poliphony, 8 harmonics/pipe. (Size: 676 kb, length: 42 másodperc) - J. S. Bach: Ich ruf zu Dir choral (full)
Matlab simulation, Stops: Diapason 8', Diapason 4', Bourdon 8', Octavbass 8', Subbass 16'. (Size: 2.7 Mb, length: 2 min 50 sec)
If you are interested in the topic, or have comments or questions, please write an e-mail to markus@mit.bme.hu.
Manufacturers of digital organs
- Ahlborn orgelbau
- Allen organs
- Baldwin organs
- Johannus orgelbouw
- Makin organs
- Prestige organs
- Rodgers organs
Research Institutes
Last modified: May 11, 2004.
Photos (c) János Márkus, DMIS


